| Paradokser i fysik
c + c = c ?
See also: English ed. of this
|

|

Illustration fra:
"Mr. Tompkins i drømmeland eller historien
om lille c, store G og lille h", George Gamow,
Gyldendals Uglebøger, 1965 ("Mr. Tompkins
in Wonderland or Stories of c, G and h")
|
 |
 |
 |
Galilei-transformationen

Tegning fra Joseph Schwartz & Michael McGuinnes: "Einstein
for begyndere", Basilisk, 1983
Et tog suser afsted med hastigheden v =
100 km/t.
En passager inde i togvognen går i samme retning som
toget kører, med hastigheden w = 3 km/t i forhold
til togvognen.
Så bevæger passageren sig i forhold til jorden
med hastigheden u = v + w
= 100 + 3 = 103 km/t.
Hvis passageren går i modsat retning af togets kørselsretning med hastigheden w = -3 km/t (minus fordi det er i modsat retning)
fås passagerens hastighed i forhold til jorden til u = 100 + (-3) = 100 - 3 = 97 km/t.
Dette princip - at addere hastigheder - kaldes Galilei-transformationen
efter Galileo Galilei (1564-1642).
Inertiens lov, inertial-systemer og relativitets-princippet
Galilei og senere Isaac Newton (1642-1727)
formulerede inertiens lov:
En genstand der ikke påvirkes af nogen ydre kraft,
vil være i hvile eller i jævn retliniet bevægelse.
Denne lov kan også benyttes til en
definition af et 'inertial-system':
Et inertial-system er et system
i hvilket inertiens lov gælder.
Men gælder inertiens lov ikke altid?
Nej, f.eks. ikke i et tog som accelererer eller drejer i
en kurve, eller på en karrusel, eller på Jorden
som drejer om sin akse. (Inertiens lov kan dog 'reddes'
ved at indføre såkaldte 'fiktive kræfter').
Har man først fundet sig et inertial-system,
kan man finde uendelig mange. Ethvert system som bevæger
sig jævnt retliniet i forhold til det først
fundne inertial-system, vil selv være et inertial-system.
I inertial-systemer gælder relativitets-princippet
(også oprindeligt formuleret af Galilei og Newton):
Alle fysiske love har samme form
i alle inertial-systemer.
Eller:
Man kan ikke internt i et inertial-system
afgøre om dette bevæger sig eller står
stille.
Kun ved at 'kigge ud' kan man afgøre om ens eget
inertial-system bevæger sig relativt i forhold til et andet
inertial-system.

Tegning fra L.D.Landau & G.B.Rumer: "Hvad er relativitet?",
Munksgaard, 1963
Nogle af eksemplerne på denne side er bl.a. inspireret
af denne bog.
En passager i et tog der kører jævnt
og retliniet, kan ikke ved eksperimenter - som f.eks. at
kaste en bold lodret op i luften - afgøre om toget
kører eller står stille. Kun ved at kigge ud
af vinduet kan det afgøres om toget bevæger
sig relativt til f.eks. perronen. Toget er et inertial-system.

Tegning fra L.D.Landau & G.B.Rumer:
"Hvad er relativitet?", Munksgaard, 1963
Hvis toget øger eller mindsker farten (accelererer positivt eller negativt) eller drejer i en kurve kan det mærkes
inde i togvognen uden at kigge ud af vinduet, f.eks. som
vist på tegningen. Toget er nu ikke et inertial-system.
Lysets paradoks og 'æteren'
James Clark Maxwell (1831-1879) formulerede
'Maxwell's ligninger' som samlede al viden om elektriske
og magnetiske felter i fire ligninger . Hans ligninger indeholdt en interessant
løsning:
Vekslende elektriske og magnetisk felter kan skabe en 'elektro-magnetisk
bølge' med hastigheden c = 300.000 km/sek i vaccuum (det stof-tomme rum). Synligt lys er et
eksempel på en sådan bølgeudbredelse, kaldet elektromagnetisk stråling.
Når vi bruger ordet "lys" i det følgende, står det for elektromagnetisk stråling i almindelighed.
Maxwell's ligninger viste også at
lysets hastighed ikke afhænger af lysgiverens hastighed
- i modsætning til hastigheden af en riffelkugle som
afhænger af våbnets hastighed (på samme
måde som ved hastigheds-additionen i passager-tog-eksemplet
ovenfor).
Også lyd har den egenskab at lydens
hastighed ikke afhænger af lydgiverens hastighed.
Lyden forplanter sig altid i et stof, f.eks. luft, og
lydens hastighed er en bestemt størrelse i forhold
til dette stof.
Det er derfor nærliggende at forestille
sig at også lys forplanter sig i et endnu ukendt 'stof'.
Dette stof kaldtes 'æteren'. Denne æter må
vi forestille os gennemtrænger hele universet, både vaccuum og de "almindeligt" kendte stoffer. (Vi kan jo se stjernernes lys selv om der næsten intet stof er mellem stjernerne og os).
(Lysets hastighed er mindre ved forplantning gennem "almindeligt" stof - dette er med til at forklare fænomener som brydning i f.eks. glas og vand).
Men så ryger relativitets-princippet
sig en tur! For så kan vi inde i en togvogn afgøre
om toget bevæger sig eller ej ved hjælp af et
lysforsøg hvor vi måler lysets hastighed inde i toget (*1):
| I et holdende tog har lyset
en hastighed på c = 300.000 km/sek i forhold til
både tog og perron.
Hvis nu toget kører med 240.000 km/sek, vil
en lysstråle udsendt af en lampe i toget i togets
bevægelsesretning have en hastighed på
300.000 km/sek i forhold til æteren og perronen,
men 300.000 - 240.000 = 60.000 km/sek i forhold til
toget.
Tilsvarende vil en lysstråle udsendt modsat
togets bevægelsesretning have en hastighed på
300.000 + 240.000 = 540.000 km/sek i forhold til toget. |
Bemærk at noget tilsvarende ikke
ville gælde ved affyring af en riffelkugle inde i
toget, fordi riffelkuglens hastighed er konstant i forhold til våbnet og derfor afhænger af våbnets hastighed når skuddet observeres fra perronen.
Indvending: Kunne det ikke tænkes
at æteren følger med toget? I så
fald ville lysets hastighed være 300.000 km/sek i
alle retninger i forhold til toget uanset om det kører
eller ej. Så ville relativitets-princippet være
reddet.
- Dette viser sig imidlertid at være i modstrid med eksperimenter
som viser at lys ikke tager del i bevægelsen af de
stoffer det bevæger sig igennem, f.eks. strømmende
vand. (Lysets hastighed er mindre end c i vand, men afhænger ikke af vandets bevægelse).
Æter-teorien er 'sær', den
kaldtes af nogle fysikere og filosoffer en 'ad-hoc teori'
- en teori som bliver opfundet for lige at løse et
bestemt problem, men som ikke ser ud til at indgå
i de øvrige teoriers sammenhæng og som ikke
fører til yderligere ny viden. Æter-teorien
betyder også at vi må opgive relativitets-princippet. Det
er derfor fristende at opgive æter-teorien, men hvordan så
finde en teori for lysets hastighed relativt i forhold til
forskellige inerital-systemer?
Æter-teorien forkastes eksperimentelt
og relativitets-princippet sejrer
I 1883 undersøgte Michelson og Morley
om lysets hastighed målt i et laboratorium afhænger
af om lysstrålen bevæger sig vinkelret på
eller parallelt med Jordens bevægelse om Solen. Hvis
æteren findes, skulle 'æter-vinden' som Jorden bevæger sig igennem, bevirke at
disse to hastigheder afviger fra hinanden.
Eksperimentet viste ingen afvigelse overhovedt.

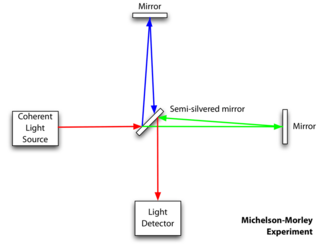
Tegningerne er fra: http://en.wikipedia.org/wiki/Michelson_Morley_experiment
(29-11-2005)
Set som et forsøg på at påvise
'æter-vinden' var dette eksperiment mislykket. Men
dets 'nul-resultat' betød at vi indser at æteren næppe eksisterer og at lysets
udbredelse ikke strider mod relativitets-princippet. Til
gengæld har vi så ingen rigtig forståelse
af lysets udbredelse - vi kan f.eks. ikke addere og subtrahere
lysets hastighed som vi gjorde ovenfor i tog-eksemplet ved hjælp af Galilei-transformationen.
Lysets hastighed ser ud til at være en absolut størrelse
i modsætning til alle andre hastigheder.
Dette tilsyneladende
paradoks skyldes måske at vi går ud fra nogle
forudsætninger ('paradigmer') som ikke holder. Måske
har vi anset noget andet for at være absolut som i
virkeligheden er relativt? Hvad kan dette 'noget andet' være?
Vi har en mistanke. Hastighed findes jo ud fra en vejlængde divideret med
et tidsinterval, så hvis hastigheder bliver "sære",
så må vel også længder og tider blive "sære" - måske relative?
I øvrigt er dette eksperiment interessant
videnskabs-historisk. Hvis man havde været i stand
til at udføre disse målinger på Galilei's
tid kunne den katolske kirke have brugt resultatet til at
stadfæste at Jorden står stille, og at Galilei's
påstand, at Jorden kredser om Solen, må være forkert. I
videnskabens udvikling står hverken eksperimenter
eller teori alene, de følges hele tiden ad i en indbyrdes
vekselvirkning.
Einsteins antagelser
I 1905 publicerer Albert Einstein (1879
- 1955) en artikel i fysik-tidsskriftet 'Annalen der Physik'.
Artiklens titel er: 'Zur Elektrodynamik bewegter Körper'
('Om bevægede legemers elektrodynamik').

Første afsnit i Einsteins artikel i engelsk
udgave (Adobe Reader pdf-fil):
On the Electrodynamics of moving bodies
Einstein viser her at Maxwell's elektromagnetiske
ligninger ikke bevarer deres form (er ikke 'invariante') ved Galilei-transformationen
mellem forskellige inertial-systemer. Det betyder at relativitets-princippet ikke er opfyldt.
Enten er der noget galt med Maxwell's teori
eller med Galilei-transformationen.
Einstein forkaster æter-teorien og
forsøger at løse problemet ved at gå
ud fra to antagelser:
- Lysets hastighed i det tomme rum
er c = 300.000 km/sek og uafhængig af såvel
lysgiverens som lysmodtagerens hastighed.
- Relativitets-princippet gælder
for alle inertial-systemer.
Af disse to antagelser er den første
om lysets absolutte hastighed den mest 'overraskende'. Konsekvenserne af de to antagelser bliver at vi må
give afkald på andre grundantagelser:
- Tid og rum er ikke absolutte, men
relative størrelser.
- Galilei-transformationen må
erstattes af en anden form for transformation
Maxwell's teori bevares, men Newton's klassiske
mekanik må revideres, da den hviler på Galilei-transformationen.
Vi må dog forvente at Newton's meget velbekræftede
teori er god nok i det 'klassiske grænseområde'
hvor hastighederne er små i forhold til lysets hastighed.
Det er bemærkelsesværdigt at Einstein i sin artikel fra 1905 ikke direkte refererer til andre videnskabelige artikler. Blandt videnskabsteoretikere og videnskabshistorikere har det været diskuteret i hvor høj grad eksperimentelle resultater versus teoretiske betragtninger spillede en rolle for Einstein ved fremsættelsen af relativitetsteorien (den 'specielle') i 1905. Einstein har selv på et tidspunkt benægtet at have været væsentligt påvirket af Michelson-Morley eksperimentet. Det væsentlige var de teoretiske betragtninger over problemet med at Maxwell's elektromagnetiske ligninger ikke er invariante ved Galilei-transformationen.
Se også: http://http://en.wikipedia.org/wiki/History_of_special_relativity (21-05-2011)
Tidsintervaller er relative (*2)
| Vi er passager i et specielt
Einstein-tog som farer af sted med 240.000 km/sek
= 0,24 mill.km/sek. Toget forlader station 1 og kører
864 mill.km til station 2.
Det tager 1 time (864/0,24 = 3600 sek).
Vi stiger på toget på
station 1 og stiller vores ur efter stationsuret.
Ved ankomsten til station 2 opdager vi at vores ur
er bagefter stations 2's stationsur. |

Figur og taleksempel er fra L.D.Landau
& G.B.Rumer: "Hvad er relativitet?", Munksgaard,
1963.
Ideen til "lys-uret" stammer vist nok oprindeligt
fra fysikeren R.P. Feynman
| Inde i toget laver vi (passageren)
et eksperiment. Vi sender en lysstråle op i
loftet fra en lampe fastgjort til togvognens gulv.
I loftet kaster et spejl lysstrålen tilbage
til lampen.
På grund af togets bevægelse vil en iagttager på perronen se lysstrålens bane helt anderledes.
Lysstrålens afgang fra
lampen og tilbagekomst til lampen er to "rum-tids-begivenheder"
som er veldefinerede for begge personer. Trods dette viser det sig nu at tidsintervallet mellem disse to rum-tids-begivenheder måles helt forskelligt for de to iagttagere. |

Figur fra L.D.Landau & G.B.Rumer:
"Hvad er relativitet?", Munksgaard, 1963.
En fejl i trekanten er dog blevet rettet i forhold til originalen.
| Set var vores synspunkt bevæger
lysstrålen sig lodret op og ned, stykket D-B-D.
Afhænger lysstrålens
bevægelse da ikke af om toget kører eller
ej?
Nej, jfr. Einsteins antagelse nr. 2, relativitets-princippet
Set fra iagttageren på perronen
bevæger lysstrålen sig langs to sider
i en ligebenet trekant A-B-C.
Lysets hastighed er c både
set fra os i toget og set fra personen på perronen..
Jfr. Einsteins antagelse nr.
1.
Da lysstrålen
bevæger sig en længere vej set fra perronen
end set fra toget, men med samme hastighed, må
tidsintervallet mellem de to rum-tids-begivenheder
set fra perronen (t) være længere end
set i toget (t'). |

| Vi beregner nu tidsintervallet
mellem de to rum-tids-begivenheder set fra henholdsvis
os og personen på perronen.
Lysets hastighed er 0,3 mill.km/sek
og lad toget køre med 0,24 mill.km/sek
Set
fra vores synspunkt i toget bevæger lyset sig
fra gulv til loft og tilbage til gulv, altså
stykket D-B-D. Lad os kalde tidsintervallet for denne
bevægelse t'.
Vi har så (**):
t' = 2BD/0,3 og heraf fås: BD = ½ x 0,3 x t'.
Set fra personen på perronen
har lampen på togvognens gulv flyttet sig stykket
A-D-C i samme tidsinterval som lysstrålen har
bevæget sig stykket A-B-C. Lad os kalde dette
tidsinterval for t.
Vi har så (**):
t = (AB+BC)/0,3 = AC/0,24
Da trekant ABC er ligebenet, dvs. AB = BC,
kan vi også skrive: t = 2AB/0,3 = 2AD/0,24
og heraf fås: AB = ½ x 0,3 x t og
AD = ½ x 0,24 x t
I den retvinklede trekant CBD
gælder
Phytagoras: AB2 = AD2 + BD2
Indsætter vi nu hvad vi
ved om trekantens sider,
får vi: (½ x 0,3
x t)2 = (½ x 0,24 x t)2
+ (½ x 0,3 x t')2
eller: (0,32 - 0,242)
t2 = 0,32 t'2
eller: (t/t')2 = 0,32 /
(0,32 - 0,242)
eller: t/t' = 10/6
Lad os antage at Einstein-toget
er BD = 0,9 mill.km højt !
Så bliver tidsintervallet
set i toget: t' = 2BD/0,3 = 6 sek.
og tidsintervallet set fra perronen:
t = 10/6 t = 10 sek. |
| Formlen for tiderne kan omskrives
til:
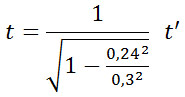
Og generelt fås:

hvor v er togets hastighed og
c er lysets hastighed.
Tiden t' er tiden for en proces
i hvile i forhold til iagttageren ('hvile-tiden' eller
'egen-tiden')
Tiden t er tiden for den samme proces i bevægelse
med hastighed v i forhold til iagttageren.
Dette fænomen kaldes 'tids-forlængelsen'
fordi t > t'. |
Hvis toget ifølge urene
på stationerne er 1 time om at bevæge sig fra
station 1 til station 2, så tager denne rejse set
fra vores (passagerens) synspunkt kun 60 min x 6/10 = 36
min. Vores ur har altså tabt 24 min i forhold til
stationsurene i løbet af denne time.
Hvis lampen på togvognens
gulv igen kan reflektere lysstrålen op, kan dette
lys-forsøg opfattes som et ur som "tikker"
hver gang lyset når tilbage til lampen. Alle
tidsprocesser må følge denne tidstransformation.
Ellers ville der komme uoverensstemmelse mellem tiderne
i forsøget og tiderne målt med andre slags
ure. Ure der bevæger sig taber i forhold til ure som
står stille. Formuleret præcist:
Ure (processer) der bevæger
sig i forhold til en iagttager vil - set af denne iagttager
- gå langsommere end ure (samme processer) som er
i hvile i forhold til en iagttager.
Passageren i toget konstaterer
at en proces (hans lys-urs "tik") tager 6 sek,
mens personen på perronen ser den samme proces tage
10 sek. Passagerens ur må derfor tabe, og det kan
passageren konstatere ved at sammenligne tidsintervallet
på sit ur med tidsintervallet mellem stationsuret
som han passerer på station 1 og stationsuret som
han senere passerer på station 2.
Men kommer dette resultat
ikke i modstrid med relativitets-princippet? Kunne passageren ud fra den iaggtagelse at hans ur taber så ikke slutte at det er ham som er i bevægelse? Kunne man
ikke sige at de langsomme ure er i "mere" absolut
bevægelse end de hurtige ure?
Og kommer vi ikke til en modstrid hvis vi "bytter om"
og - i overensstemmelse med relativitets-princippet - opfatter
situationen sådan, at passageren i toget ser perronen
fare forbi i modsat retning?
Nej, for de to måder
at opfatte situationerne på er ikke "symmetriske".
Vi bruger ikke to, men tre tidsmålere når vi
sammenligner tiderne. Passageren sammenligner sit ur med
to forskellige ure på to forskellige steder (stationerne).
Hvis vi "bytter om" må det se således
ud:
Passageren i toget ser perronen
fare forbi (i modsat retning). Personen på perronen
passerer først et ur i forenden af toget, senere
et ur i bagenden af toget.
Personen på perronen
laver et lys-ur som "tikker" på 6 sek. Passageren
i toget konstaterer at "tikkene" tager 10 sek.
Perron-personens ur må derfor tabe, og det kan perron-personen
konstatere ved at sammenligne sit ur med tidsintervallet
mellem toguret som han passerer i forenden af toget med
toguret som han senere passerer i bagenden af toget.
Også længder bliver relative
Lad os se på den afstand vores tog
tilbagelægger.
| Afstanden mellem station 1
og station 2 er 864 mill.km og rejsen tager 1
time når togets fart er 0,24 mill.km/sek.
Men for passageren i toget tager
det jo kun 36 min eller 2160 sek at se vejlængden
mellem stationerne fare bagud. Han må jo så
komme frem til at afstanden mellem stationerne er:
0,24 mill.km/sek x 2160 sek
= 518,4 mill.km
Strækningen mellem stationerne
ser altså kortere ud set fra toget end set fra
jorden. Forkortelsen sker her med faktoren 6/10. |
| Formlen for længderne
ser generelt således ud:

hvor v er togets hastighed og
c er lysets hastighed.
Længden L er længden
af en strækning i hvile i forhold til iagttageren
('hvile-længden')
Længden L' er længden af den samme strækning
i bevægelse med hastighed v i forhold til iagttageren.
Dette kaldes 'længde-forkortningen'
fordi L' < L. |
Længden af en genstand
ses at være kortere når genstanden bevæger
sig i forhold til en iagttager end når den er i hvile.
I vort tog-eksempel er L' = 864 mill. km og L = 518,4 mill. km.
Ligesom tids-forlængelsen
er længde-forkortningen ikke i modstrid med relativitets-princippet.
En person på en perron vil på samme måde
konstatere at længden af f.eks. toget der passerer,
vil være kortere end den længde toget måler
set fra en passager på toget.
Lad os sige at toget er 5,4
mill.km langt, (hvilelængden set fra toget). Set fra
perronen vil dets længde så være
5,4 mill.km x 6/10 = 3,24
mill.km.
Men hvordan kan personen på
perronen måle togets længde?
Personen på perronen
sætter en fotocelle op som giver en elektrisk impuls
når togets forende passerer og en ny elektrisk impuls når
togets bagende passerer. Denne proces (registrering af de to impulser) er i hvile i forhold til perronen, og tiden
det tager viser sig at være 13,5 sek.:
Så kan personen på perronen slutte at togets
længde er togets hastighed gange denne tid:
0,24 mill.km/sek x 13,5 sek
= 3,24 mill.km.
Hvor ved vi fra at der set fra perronen går
13,5 sek mellem de to impulser? Lad os kalde denne tid for ?.
Set fra toget bevæger
fotocelle-processen sig med togets hastighed bagud, og tiden
for processen bliver tidsforlænget med faktoren 10/6.
D.v.s. passageren i toget konstaterer at tiden mellem at
togets forende og togets bagende passerer fotocellen må
være ? sek x 10/6.
Men passageren kan jo også regne den tid ud ved at
benytte togets hvilelængde:
5,4 mill.km / 0,24 mill.km/sek
= 22,5 sek.
Så vi har at ? sek x 10/6 = 22,5 sek, eller at ? sek
= 6/10 x 22,5 sek = 13,5 sek.
Muon-paradokset
Muoner er elementar-partikler (undertiden
kaldet 'tunge elektroner') som dannes når den kosmiske
stråling rammer atmosfæren i en højde
på ca. 10 km over Jordens overflade.
Man ved fra forsøg i laboratorier
at muonen har en levetid på 2,2 10-6 sek
(hvorefter partiklen henfalder til andre partikler).
Muonerne dannet af kosmisk stråling
kan registreres ved Jordens overflade.
Dette er et paradoks, for muonen lever ikke længe
nok til at nå ned til os - selv med en hastighed på
lysets hastighed!
Hvordan kan dette paradoks opløses?
- Ved hjælp af relativitets-teorien.
| Muonens levetid: t' = 2,2
10-6 sek, målt for muoner i hvile
Muonens hastighed: v = 0,999 c, hvor c er lysets hastighed
Set fra klassisk fysisk synspunkt kan muonen
i sin levetid tilbagelægge afstanden:
L = 0.999 c x 2.2
10-6 s = 0.659 km
- 659 meter ! - altså slet ikke langt nok til
at nå ned til os fra højden 10 km hvor muonen bliver dannet.
Set fra muonens hvilesystem har
muonen egenlevetiden t'.
Set fra Jordens system svarer denne tid til den forlængede
levetid t:

Faktoren foran t' kaldes ofte
'gamma'.
Med v = 0,999 c bliver gamma her: 22,4.
Vi får så levetiden
i Jordens system:
t = 22,4 x 2,2 10-6
sek = 49,2 10-6 sek
Set fra Jordens system kan muonen
nå at tilbagelægge afstanden:
L = 0,999 c x 49,2
10-6 sek = 14,7 km
- altså nok til at nå ned til os.
Vi kan også se dette fra
muonens 'synspunkt':
Muonens egenlevetid er t' = 2,2
10-6 sek, og på sin rejse ned mod
Jorden 'ser' muonen den tilbagelagte strækning passere
bagud med hastigheden 0,999 c. Denne strækning
L' er forkortet i forhold til strækningen set
fra Jorden som er ca. L = 10 km:

Vi får strækningen
set fra muonen til:
L' = 1/22,4 x 10 km = 0,447 km = 447 m.
Muonen kan i sin egenlevetid
nå at tilbagelægge 0,66 km, så den
kan sagtens nå ned til os. |
 |
Tvillinge-paradokset
To tvillinger, Abel og Bolette på
15 år tager afsked med hinanden på afgangs-pladsen
for rumskibe. Tvilling Abel stiger ind i rumskibet og rejser
til en fjern stjerne med stor hastighed. Abel vender tilbage
til Jorden og Bolette tager imod ham. Abel mener at han
har været på rejse i 1 år (egen-tiden
t'), han er blevet 16 år, men hans søster er blevet 20 år ældre
(tiden t), hun er nu 35 år gammel. Det bekræftes når de to tvillinger
sammenligner deres ure, Abels ur er mange år bagefter!
Hvis Bolette havde kunnet følge Abels ur, f.eks.
under en del af udrejsen ville hun også forvente dette
ifølge relativitetsteorien. Abel har ikke mærket
noget specielt, han synes bare der er gået 1 år.
Men ifølge relativitets-princippet
må vi også kunne se situationen fra Abels synspunkt.
Abel ser Jorden fjerne sig bagud med stor hastighed og senere
vender Jorden - og Bolette - tilbage igen. Abel må
derfor mene at det er Bolette der har bevæget sig
mens han har været i hvile. Derfor må det være
Bolette der er blevet 16 år mens Abel er blevet 35
år.
Denne problemstilling minder om den tidligere
nævnte med togrejsen mellem de to stationer
versus stationens rejse i modsat retning. Men i modsætning
til det tidligere eksempel hvor der indgik 3 tidsmålere
(et ur der bevæger sig mellem to andre ure), indgår
der i dette problem kun 2 tidsmålere - de to tvillingers
ure - og de to måder at betragte begivenhederne på er symmetriske.
Her er der tilsyneladende virkelig et paradoks,
for de to tvillinger kan jo i begge udgaver af historien
sammenligne deres ure direkte - og så kan begge resultater
jo ikke passe. Viser Abels ur 16 år og Bolettes 35
år eller omvendt - eller noget helt andet?
Paradokset opløses når vi
erkender at vi ikke har holdt os indenfor relativitetsteoriens
rammer - eller rettere, den specielle
relativitetsteori, formuleret af Einstein i 1905.
Denne teori beskæftiger sig nemlig kun med inertial-systemer,
altså systemer som bevæger sig med jævn
retliniet hastighed i forhold til hinanden. For at komme
tilbage til Jorden må Abel jo på et tidspunkt
vende om og bevæge sig i modsat retning. Herved ændrer
han sin bevægelsesretning (han får en acceleration),
og under denne ændring er
hans system ikke mere et inertial-system.
Først ud fra den
almene relativitetsteori fra 1915 kan problemet forstås.
I denne teori påvises det at tid og rum også
ændres p.gr. af gravitations-felter og accelerationer.
Tages der højde for Abels 'omvending' viser det sig at kun den
første version af historien kan bekræftes. Når tvillingerne mødes igen er Abel blevet 16 år og Bolette 35 år.
Tids-effekterne af relativitetsteorierne
benyttes ofte i Science Fiction romaner (rafineret af
f.eks. forfatteren Ursula K. Le Guin, se Litteratur). Der sker sære
ting, men hvis man i øvrigt holder sig indenfor relativitetsteorierne
bliver der ikke tale om at kunne rejse tilbage i tiden og
slå sine egne forældre ihjel! Heldigvis. Følgende
Limerick citeres i Martin Gardners bog om relativitetsteorierne,
se Litteratur, som eksempel på noget der ikke
kan lade sig gøre:
There was a young lady named Bright
who traveled much faster than light.
She started one day
in the relative way,
and returned on the previous night.
c + c = c ! - og Lorentz-transformationen
Hov, det var jo dette paradoks der gav
titel til dette afsnit om relativitetsteori.
En konsekvens af den specielle relativitetsteori
er at Galilei-transformationen må opgives og erstattes
af en ny form for transformation kaldet Lorentz-transformationen.
H.A.Lorentz (1852-1928) foreslog denne transformation for
bl.a. at forklare at legemer bliver sammenpressede når
de bevæger sig igennem æteren. Einstein modificerede
Lorentz's ligninger og gjorde deres betydning mere generel,
de udtrykker ikke en effekt af æteren - for den eksisterer
ikke - men en egenskab ved rum og tid.
De tidligere formler for tidsforlængelse
og længdeforkortning er specialtilfælde af Lorentz-transformationen
hvor rum og tid stadig holdes adskilt. De fuldstændige
formler indeholder en blanding af rum og tid som ikke kendes
fra den klassiske fysik.
Maxwell's ligninger viser sig at være
invariante overfor Lorentz-transformationen, dvs. de bevarer
deres form i alle inertial-systemer. - det gjorde de ikke
under Galilei-transformationen. Det var jo bl.a. det der
satte Einstein igang med hans relativitets-projekt.
Nye transformations-formler for rum og
tid må også betyde nye formler for hvordan hastigheder
"adderes".
Ifølge Galilei-transformationen
så det således ud:
u = w + v
hvor w var passagerens hastighed
i forhold til togvognen, v togvognens hastighed i forhold
til jorden og u passagerens hastighed i forhold til jorden.
Ifølge Lorentz-transformationen
skal de samme hastigheder "adderes" således:

Lad os prøve med w = ½c og
v = ½c. Så fås: u = c/1.25 = 0,8 c.
Og lad os prøve med w = c og
v = c. Så fås: u = 2c/2 = c !
Så hvis i et tog en lysstråle (eller noget andet) bevæger sig med hastigheden c i forhold til toget, og hvis toget bevæger sig med hastighed c i forhold til perronen, så vil lysstrålen bevæge sig med hastighed c i forhold til perronen.
Dette skulle jo også gerne blive
resultatet, jfr. Einsteins 1. antagelse.
Korrespondens med den klassiske fysik
Hvad med Galilei-transformationen og den
klassiske fysik? Skal alt det bare smides væk?
Nej, den klassiske Newton'ske mekanik er stadig god nok,
blot vi holder os til hastigheder som er små i forhold
til lysets hastighed.
Hvis w og v er så små i forhold til c at produktet w
v er meget mindre end c2 (w v << c2),
så bliver w v/c2 tæt på 0,
og Lorentz-formlen går over i Galilei's gode gamle
formel for hastigheds-addition.
I den generelle relativitetsteori opstår
der tilsvarende 'u-klassiske' effekter p.gr. af store gravitations-felter
eller store accelerationer. Men Newton's gravitations-teori
er stadig god nok hvis gravitationskræfterne ikke
er for kraftige.
Det samme gælder den anden store
teori i moderne fysik, kvanteteorien. For partikler (og
energier) som er store, går kvantefysikkens resultater
over i den klassiske mekanik. Niels Bohr formulerede dette
i sit 'korrespondens-princip'.
Man kan sige at den moderne fysik er en
revolution i forhold til den klassiske fysik, fordi den
udskifter de gamle paradigmer om f.eks. rum, tid, partikel-baner
og årsag-virkning med nye. Men for små hastigheder,
små masser og store partikler og energier 'korresponderer'
den nye fysik med den gamle.
| (*1) (*2) Hurtige tog, lange strækninger
Tog-eksemplerne benytter urealistiske (for tog) store hastigheder og dimensioner samt urealistiske (for jernbaner) lange strækninger. Dette er nødvendigt, på grund af lysets store hastighed, for at vise relativistiske effekter med "hverdagsagtige" tider af størrelsesordenen minutter.
Man kunne også have valgt at bevare realistiske mål for hastigheder og afstande og så i stedet for forestille sig at lysets hastighed er ganske lav, f.eks. 10 km/t - svarende til hvad George Gamow har gjort i sin bog "Mr. Tompkins i drømmeland" (se Litteratur). |
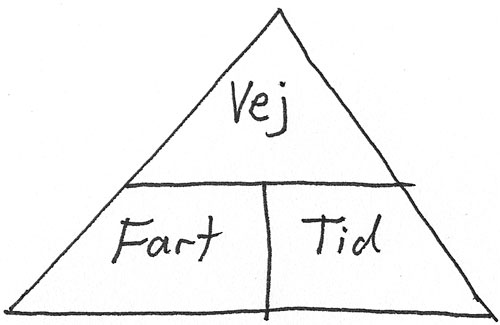 (**) "Fart-trekanten" (**) "Fart-trekanten"
fart = vej/tid
vej = fart x tid
tid = vej/fart |
Litteratur:
L.D.Landau & G.B.Rumer: "Hvad
er relativitet?", Munksgaard, 1963
Martin Gardner: "Relativitetsteorierne",
Hasselbalch, 1964 ("Relativity for the Million")
George Gamow, "Mr. Tompkins i drømmeland
eller historien om lille c, store G og lille h", Gyldendals
Uglebøger, 1965 ("Mr. Tompkins in Wonderland
or Stories of c, G and h")
Joseph Schwartz & Michael McGuinnes:
"Einstein for begyndere", Basilisk, 1983 ("Einstein
for Beginners")
Leo Sartori: "Understanding Relativity: A Simplified Approach to Einstein's Theories", University of California Press 1996
Ursula K. Le Guin: "Semley's Necklace" i "The Wind's Twelve Quarters", Bantam Books 1979
Se videre: Paradokser
i fysik - Kaos i solsystemet?
See more: Paradokser
i fysik - Lorentz Transformation
|